■■■各限月毎加重平均とボラティリティ　■■■

　東京小豆の最近10年間の加重平均は12,309円です。
つまり、よく相場は、「安きを買い、高きを売れば儲かる」といわれますが、
その安い高いの基準がこれです。

おおまかにはこの数字だけでもよいのですが、先物には限月というものが存在します。

同じ小豆でも12,000円など価格の意味する度合いがかわってきます。
例えば、旧穀と新穀の格差が1,000円＋サヤという具合に各要因が交錯するからです。
もう少し詳しく、限月毎に加重平均とボラティリティを調べてみましょう。

■東京小豆　各限月毎の加重平均とボラティリティ

1986-1995年の10年間にて

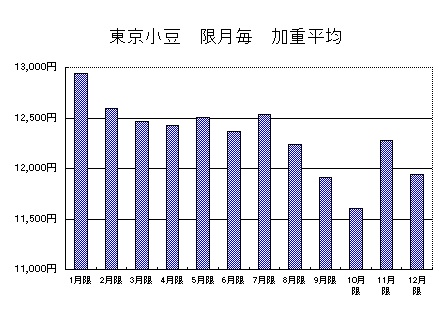
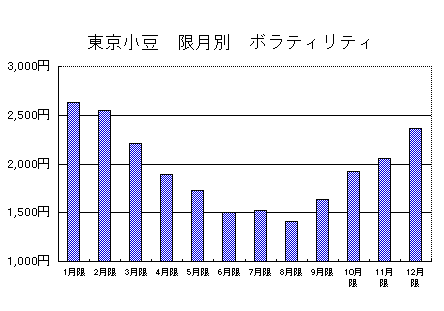
　限月　　加重平均　　ボラティリティ
01月限　　12,942円　　　2,631円
02月限　　12,594円　　　2,551円
03月限　　12,468円　　　2,206円
04月限　　12,422円　　　1,888円
05月限　　12,504円　　　1,730円
06月限　　12,371円　　　1,501円
07月限　　12,537円　　　1,520円
08月限　　12,237円　　　1,415円
09月限　　11,908円　　　1,636円
10月限　　11,602円　　　1,926円
11月限　　12,281円　　　2,061円
12月限　　11,937円　　　2,368円

分かりやすくグラフにしてみましょう。

※ボラティリティとは、統計学でいう「標準偏差」のことで、
データの散らばりぐらいを知るための指標です。全データの
平均値と個々のデータの差を二乗したものの合計をデータ数
で割ったもの（分散）の平方根です。

　要するに

ボラティリティがある　＝　人気がある　＝　動きが期待できる
ボラティリティがない　＝　人気がない　＝　動きが期待できない

　　　ということです。

　　　東京小豆の加重平均は01月限が一番高く、10月限が一番低い
　　　天候相場の時期に存在する限月はボラティリティが高く
　　　需給相場の時期に存在する限月はボラティリティが低い