■日本語版への序文
今から15年以上も前のことになるだろうか。任意のパラメータに対してトレーダーが買うべき「最適な」枚数を割り出す方法を模索して、私は数カ月にわたる悪戦苦闘の真っただ中にいた。通常は結果が2つしかないギャンブルに適用されるいわゆる「ケリーの法則」というものを、トレード流列に応用する方法を見いだそうとしていたわけである。平凡な毎日を送るわが身にとって、これほど楽しい刺激はなかった。その間の数カ月というもの、この数学問題は寝ても覚めても頭から離れず、私は夢中になって考え続けた。ある日のこと、意外にもシンプルな解答が突如ひらめいたのである。そのとき脳裏に浮かんだものはひとつ残さずメモを取り、記録した。本書はそのときのメモをまとめたものである。
当初はこのシンプルな解答が現実世界でも十分通用するものだと楽観視していた。確かにそれは数学的に「最適な」解答ではあった……。
収益率を、しかも過去のトレード流列の収益率を最大化するという意味では。
しかし、大地がわれわれの足元で常に動いているように、現実世界も絶えず変化しているのだ。
これらの公式を現実世界に応用するに当たっては、自分自身はもちろんのこと、ほかの多くの人にも試用してもらった。大概の場合は素晴らしくうまくいったが、喜びもつかの間。またしても大地がわれわれの足元で動いていることを実感させられるはめになった。
公式そのものに問題があるわけではない。しかし、いざ応用しようとすると、2つの厄介な問題に阻まれて立ち往生してしまうのだ。問題のひとつは、公式への入力として用いた過去のデータが変化してしまうこと、そしてもうひとつは、これらの公式を導入しようという側に相応の覚悟がないことだった。
本書で紹介する公式は出発点にすぎない。厳密な手法というよりも、定量化問題をどう扱わなければならないかを考えるための手段といったほうがよいだろう。本書は、ひとつの口座においてトレード可能な「相対」量を考えるための枠組み、すなわちポートフォリオ構築のための枠組みの基礎を学ぶうえで役立つものである。少なくとも私は本書をそのように位置付けている。
本書は理論についての本ではない(本書で提示する公式は単なる仮説ではなく、すべて証明可能)。本書は実用化を目指すための基礎となるものであり、特にアグレッシブなトレーダーを対象とするものである。
これらの公式を導入しようという人々を見て私が感じたことは、人は一定の痛みの範囲内で収益率を最大化することを求めているということである。しかし、痛みを一定範囲内に抑えることは、本書の趣旨とするところではない。
とはいえ、人間というものは弱いものであり、結局は耐えられる痛みには限度があるのが現実だ。
本書は収益率を最大化するための数学の基礎について書かれたものではあるが、痛みに対する限度は設けていない。個人が絶え得る痛みの範囲内で収益率を最大にするための方法は、今後の研究課題となるであろうが、そういった将来的な研究を進めるための基礎固めとしても、本書はきっと役立つはずである。
2005年8月
ラルフ・ビンス
■監修者まえがき
本書は、株式や先物の運用における最適なマネーマネジメント手法を解説した『Portfolio Management Formulas』の邦訳である。本文中にあるように、いかに優れた運用ストラテジーをもってしても、レバレッジの選択を誤れば、良好なパフォーマンスを期待することはできない。最終的な損益は、ひとえにストラテジーの優位性とマネーマネジメントの巧拙にかかっているのである。
さて、資金運用において結果の優劣を決定的に分けるものとは何であろう? 奇妙に聞こえるかもしれないが、私の見たところ、それは個々人が日々納得してトレードを行えているか否か、ということに尽きる。そのためにはとりもなおさず、トレードに当たって「不安がない」ことと「手際がよい」ことが絶対に必要である。このどちらかを欠いた不本意で無責任な運用からは、生じた損益の多寡に関係なく、後味の悪い思いが残るだけである。
クオンツ運用であれ、ボトムアップの定性的な判断による運用であれ、いわゆる情報というものは常に不確実で曖昧なものであるが、好むと好まざるとにかかわらず、私たちはそういったものに依拠して分析や考察を行わざるを得ない。したがって、自分自身が不安定な状態では、なおのことまっとうな結果はおぼつかないのである。
逆に、迷いがなく、かつ手際よくトレードが実行できていれば、目先の損益に拘泥することなく常に落ち着いて運用に取り組める。さらに、そういったアプローチは運用における技術や感覚を向上させ、非定常的なマーケットにおいて私たちに柔軟で臨機応変な対応を可能とさせるのである。いかなる状況においても適切な行動がとれるという自信や、短期的な結果に心理状態が左右されない謙虚さこそ、個人投資家や機関投資家を問わず、運用者が目指すべきものである。
この書籍で著者のラルフ・ビンスは数学的に最適とされるレバレッジの決定方法(オプティマルf)を示した。書かれている内容を把握するには初歩的な数学の知識を必要とするものの、昨今のコンピューター(PC)をもってすれば、だれでも簡単に必要な計算を行うことができる。そして実際にトレードコンテストにおいてこのマネーマネジメント手法を採用したラリー・ウィリアムズは1年で資金を100倍以上にし、ビンスの理論の正しさを証明してみせた。読者におかれても、オプティマルfを理解することで、マネーマネジメントに関する迷いは払拭され、自分の持つ運用手法のエッジを限界まで引き出すことができるであろう。
原書の出版以来長きにわたり名著の誉れ高かった書籍の邦訳を世に出せることは、関係者一同の誇りとするところである。できるかぎり末永く多くの人に読み継がれ、それが個々人の納得のいくトレードにつながることを願う。
最後に、翻訳に当たっては以下の方々に心から感謝の意を表したい。山下恵美子氏には正確な翻訳をしていただいた。そして阿部達郎氏にはいつもながら丁寧な編集・校正を行っていただいた。また、本書が発行される機会を得たのはパンローリング社社長の後藤康徳氏の慧眼と責任感の強さ、決断に負うところが大きい。
2005年9月
長尾慎太郎
■序文
本書は数学的ツールについて書かれたものである。数学的観点から言えば、これらのツールはトレーダーにとってはきわめて重要であり、したがって本書を読むことで彼らの市場観はガラリと変わるだろう。
読者対象としては主として先物トレーダーを想定しているが、いかなる市場の参加者にとっても役立つ内容である。読者がどの市場の参加者かは知るよしもないが、どういった市場の参加者であれ、本書で紹介するツールをすべて備えている人はおそらくはいないだろう。これから徐々に明らかになるが、本書で紹介するツールはどのひとつを欠いても大きな代償を支払うことになるような重要なツールばかりである。
トレーダーにとっての重要なツールとしてまず挙げられるのが、トレードの選択、あるいはシステムトレーダーの場合はシステムの選択である。これは大部分のトレーダーが心血を注ぐ部分であり、そのためこの分野について書かれた書籍は多い。ただし本書では、トレードの選択やシステムの選択に関連する内容は、システムの問題点や落とし穴に対する改善方法について述べるに留めている。こういった問題点や落とし穴は、主としてトレーディングシステムの構築にコンピューターを用いることの代償として発生する場合が多い。
本書が焦点を当てるのは、トレーダーたちになおざりにされがちなツールである。そのひとつが、量である。本書では任意のシステムを使って任意の市場でトレーディングする際の適正なトレード量の計算方法について詳しく解説する。量というものがトレードの選択に負けず劣らず重要であることが明らかになるにつれ、トレーディングに対する読者の考え方は変わってくるはずである。どちらもトレーディングには欠かせない重要な概念なのである。本書を読み進めていくうちに、トレードをするうえで重要なのは前のトレードで勝ったか負けたかではなく、正しい量でトレードしたかどうか、であることも明らかになるだろう。ファンドマネジャーの多くがS&P500指数に打ち勝つことができないのは、正しい量でトレードしていないことが大きな理由のひとつである。指数は収益の再投資問題とは無縁だが、ファンドマネジャーはそういうわけにはいかないのである。
トレード選択のための優れたツールと、量を決定するための適切なツールの次に必要になるのが、収益率の相関についての概念である。分散化とも呼ばれるこのツールもまた、トレーダーたちになおざりにされがちなツールのひとつだが、重要さにおいては最初の2つに引けをとらない。本書では分散化プロセスを定量化することで、どの市場およびどのシステムでトレードすればよいかだけでなく、どのように分散化すればよいか――すなわち、それぞれの市場でトレードすべき正しい量――についても明確にする。分散化をリスクを避けるための道具としかとらえていないトレーダーは多いが、こういった意味では分散化は残念ながら正しく理解されているとは言えない。分散化は、単にトレーディングに内包されるリスクを緩和するだけでなく、それ以上の機能を持つものである。分散化は正しく行えば、パフォーマンスの向上にも貢献する。例えば、これから本文で示していくが、同じ期間に利益を出したマーケットと損失を出したマーケットとを組み合わせることで、利益を出したマーケット以上の収益率を達成することも可能なのである。
なおざりにされてきた2つのツール――量と収益の相関――については、それがトレーダーにとっていかに強力なツールであるかということも、これらをなおざりにすることで支払わなければならない代償がいかに大きいかということも、ほとんど理解されていないと言えよう。またこれら2つのツールは、適切なトレードまたはシステムの選択とともに、マネーマネジメントの中核をなすものでもある。つまり、これまでに述べてきた3つのツールは、市場トレーディングで成功するためには絶対不可欠のものばかりなのである。これらのツールのいずれも用いることなく成功した例もあるが、それが偶然の賜物でしかないことも、次第に明らかになるだろう。
本書の読者は、マネーマネジメント・ツールによって示される方法そのものよりも、概念的に考えることの重要性に気づく機会を与えられることにもなる。本書では、トレーディングシステムが生み出すトレード流列を非定常分布として見る考え方についても説明するが、この概念は、システムに波があるのはそのトレード流列が非定常分布に従うことが原因であることを理解するうえできわめて重要である。自由市場で売買される銘柄の価格もトレード流列と同じ性質を持つ。自由に売買される銘柄のチャートを見ると、価格がランダムに形成されていると思われる時期と、強力な非ランダム要素(例えば、10日連続でサーキットブレーカーが発動する)が明らかに存在していると思われる時期とがあるが、こういった現象が生じるのは価格が非定常分布に従うことが原因である。非定常分布の概念を理解することで、仕掛けや手仕舞いの効果的な方法ばかり考えるのではなく、これまでとは異なるより生産的なものの見方ができるようになっていることだろう。
最後に、本書を読むうえでぜひとも念頭に入れておいていただきたいことがある。本書のテクニックを使って口座をより長期的に成長させるための要素のひとつとして、大きなドローダウンは避けられない、という事実である。数学的に最適な方法で口座を管理しようという場合、大きなドローダウンは残念ながら避けて通ることのできない現実なのである。しかし、本書の読者は大部分のトレーダーとは違って、トレーディングの過程で大きなドローダウンに遭遇しても、心の準備ができているためにけっして慌てふためくことはないはずだ。さらに、いかに優れたトレーディングシステムを使っていても、トレーディングをやめたくなる時期が必ずあるということも、分かってくるだろう。そこそこのシステムならば、途中でトレーディングをやめるのは賢い選択とはいえない。本書を読了した読者ならば、ほとんどのトレーダーがトレーディングをやめたくなるような局面においても、けっしてギブアップするようなことはしなくなるはずである。パンチを手控えるのは、繰り出すよりも多くのスキルを必要とするのである。
1990年6月 オハイオ州、シャグリンフォールズにて
ラルフ・ビンス
■序論――本書について
トレーディングの経験もあるし、自分なりに勝てると思う方法も一応は持っている。こんなとき、次のステップとしてあなたは何をすべきだろうか。
本書は、トレーディングに対する考え方をガラリと変えるものだ。もちろんあなたには、マネーマネジメント、つまりリスクと報酬に対する自分なりの考え方があるかもしれないし、本書で扱う題材は、あなたにとってためになるものもあれば、つまらないもの、あるいはがっかりさせられるものもあるかもしれない。しかし、あなたがどう思おうと、あなたが自分なりに勝てると思っている方法でトレーディングを成功させるためには、本書の内容を理解し実践することが絶対不可欠である。本書ではその理由を数学的な観点から解説する。
本書が焦点を当てるのは、有利な不確実性(これは1989年にR・C・ウエントワースが私信の中で初めて使った言葉)を持つ環境下での幾何的成長の最大化問題である。言い換えるならば、ひとつひとつの事象にはリスクはあるものの、事象全体でみれば有利な状況にある場合、幾何的成長を最大化するにはどうすればよいか、ということになる。本書ではこの問題をトレーディングというひとつの分野に的を絞って議論するが、この他にも応用が見込める分野は多数ある。
本書で扱う数学の多くは、例えば次のような幾何的成長関数にも応用可能である。
- 細胞の増殖または体力の増強
- 広告による売上げの伸び
- 放射性物質の崩壊
- 医薬品の半減期
- 化学反応の変化
- 体温の低下
- 人間、動物、植物、細菌、ウイルスの個体数の増加や、こういった集団内部における伝染病の拡大
上のような例を挙げれば、枚挙にいとまはない。
しかし、本書で扱うのは資本の幾何的成長関数のみである。関連する数学を検証し、ほかの条件も考慮したうえで、資本の成長を最大化するための方法を開発する。市場参加者たちはこれを「マネーマネジメント」と呼ぶ。前述のように、幾何的成長関数の応用分野はきわめて広い。本書で扱うのはそのほんの一部にすぎないことを銘記しておきたい。
市場に携わる人々の中には、マネーマネジメントに対する間違った考え方を持っている人が少なくない。しかし幸いにも、マネーマネジメントには数学的に正しい考え方というものが存在する。読者には多くのトレーダーやファンドマネジャーたちのあやまちを繰り返さないためにも、マネーマネジメントに対する数学的に正しい考え方を本書を通じてしっかりと身につけていただきたい。
本書で提示するアイデアの多くは、先物市場に携わる人々とのプログラミング経験を通して私が独自に開発したものである。事の始まりは1988年の中ごろにさかのぼる。私があるトレーダーのために作成したプログラムのひとつに、どうにも理解しがたい例外が発生したのだ。ある金曜日の夕方間近のことだった。私の作ったプログラムはある期間に利益を上げているにもかかわらず、そのプログラムで管理していた口座は同じ期間に利益を上げていないことが判明したのである。プログラムには何の問題もなく、それが発するシグナルはすべてキャッチしたにもかかわらずである。なぜこんなことになったのか。私にはどうしても理解できず、その日はこの問題が脳裏から離れなかった。
しかし翌朝には、その理由を説明できる理論と数式のすべてが頭の中にまとまっていた。本書はそこにたどり着くまでの思考の軌跡をまとめたものである。本書では、数学的に見た将来のパフォーマンスを最大化するためにはトレーダーやファンドマネジャーはどういった方法で口座を管理するべきなのかを、完全でかつ統一された形でまとめることを目指した。当然ながら既成概念が登場することもしばしばあり、かといってすべてを網羅することは不可能であるため、読者には書かれていない内容を補充しながら読み進めるといった作業を強いることになるかもしれない。しかし本書の目的は、このテーマあるいは類似のテーマについてすでに類書に書かれたことを繰り返すことではなく、それらを読者の関心が高まるような形で提示するとともに、時代が要求する新しいテーマを提供することにあることを、ご理解いただきたい。
私は最初このテーマについて本を書くつもりはなかった。しかし、この問題を解決するための数学に取り組んでいるうちに、5分やそこらの会話ではとても説明し尽くせない解を見いだすに至り、その解の性質から(つまり、ひとつの解から次の解が導き出されるといった具合に、解全体が連鎖的に構築されていくということ)、一冊の本にまとめることになったというのが本書執筆に至った経緯である。すでにお話ししたように、本書は最初は単なるコンピュータープログラムのバグだと思っていたものをきっかけに、その原因を究明していった結果、必然的に生まれたものである。
「マネーマネジメント」という言葉を聞いたとき、それがドローダウンが発生しないようにすること、あるいは減らすことを意味すると考える人は多い。それが間違った考え方であることは、本書を読めばはっきりする。市場で資金を最大限に生かそうと思えば、大きなドローダウンは絶対に避けられないのである。
本書で提示するアイデアは、金儲けができることを保証するものではなく、公式も、無から大金を生み出す手っ取り早い方法を示すものではない。有利な状況のときに、予想されるリスクに対する期待報酬の比率を数学的に最大化する方法を示すことが、本書の目指すところである。有利な状況を作りだせるかどうかは、あなた自身の問題である。また本書は、あなたがすでに市場で金儲けできる能力があること、そして有利な不確実性を持つ環境で資産運用を行っていることを前提としている。
◆クオンツの世界への誘い
コンピューターを使った市場分析は、今や、オシレータや平均、トレーディングシステムを含むいかなる数値的テクニックをも凌駕するほどの発達ぶりを見せている。コンピューターを駆使したありとあらゆる最適化やシミュレーションが試みられた今はっきりしたことは、聖杯はまだ見つかってはいないということである。
そこでお奨めしたいのが、戦略ゲームの雄として今注目されているクオンツ分析である。これは、「数字を入れてみる」ことを品質管理の新しい定義として取り入れた概念であり、何かに数字を入れてみれば、少なくともそのプロセスに対する何らかの理解は得られるはずだという考え方が根底にある。クオンツたちの市場に対する考え方は、リスクマネジメント戦略をトレーディングの基本に据えるというものである。
現在の市場分析はまさにこの方向に進もうとしている。老練な「高僧」たちの直感に頼ることなく、コンピューターを駆使することでマジックではなくて数学的に確かな方法で市場に打ち勝とうとするアプローチ。それがクオンツ分析である。本書もジャンルとしてはクオンツ分析の範疇には入るものの、その主流をなすものではないことを断っておきたい。
注意していただきたいのは、リスクマネジメント戦略という言葉がが必ずしもローリスクを意味するとは限らないということである。むしろその反対の意味合いが強い。本書で紹介するアプローチは予想される損失に対する期待利益の比率を最大化することに重点を置いている。したがって、予想される損失は不快なほど高くなる場合も多い。
全般的に言えば、予想される損失はほとんどの人のリスク回避度をはるかに上回るものになる。例えば、本書で紹介したツールを採用した場合、提示される最適なトレード量が現在の2倍にもなることがあるかもしれない。そうなればリスクが許容範囲を超えてしまうため、トレーダーはツールから導き出された結果には従わず、現在と同じトレード量を維持しようとするだろう。こうすることで、リスクは最適量でトレードした場合の半分で済む。しかし、期待利益も半分で済むかというと、そういうわけにはいかない。この場合の期待利益は半分を下回ってしまうのである。
最後に、本書で紹介するアプローチは漸近優位確率的に考えると成り立つことを前提にしていることに注意していただきたい。すなわち、予想される損失に対する期待利益の比率は長期的にに見れば最大化されるということである。もっと分かりやすく言えば、ここで導き出される結果は一般に何かを無限回行えばそういった結果になるということである。
◆本書で扱わないもの
本書で扱う題材は最初は理解しづらいかもしれないが、複雑なものは何ひとつない。各章が前章の内容の上に構築されていくという教科書形式を採っているので、1章から順に読み進めていただきたい。
説明はできるだけ簡潔にかつ端的に行うように心がけた。複雑な現象も論文調は避け、できるだけ分かりやすい方法で過不足なく説明できるように努めた。その結果、「より高度な内容」については十分に証明できていない場合もある。理由は次の2つに分けられる。
- その現象がまだ完全に解明されていない。
- その現象を不完全に(そしてその結果、おそらくは不正確に)理解するだけでも、複雑で専門的な説明を延々と行う必要がある。
その代表例が正規確率分布である。本書で扱う事象はすべて正規確率分布に従うと仮定している。こうすることで、さまざまな統計ツールが使えるようになるからである。先物価格にもこういった統計ツールを用いるが、先物価格は実際には正規確率分布には従わない。先物価格の分布については、安定paretian族の分布に従うと主張する人もいれば、t分布(スチューデントの分布)に従うと主張する人もいたりといった具合に、人によって考え方は異なる。しかし、t分布が対称分布であるのに対し、先物価格の分布が対称的にはならないことからすれば、先物価格はt分布に従わないことだけは確かである。一方、安定paretian族分布はほとんど理解されていない。その理由を徹底究明しようと思えばできないことはない。ほかの分布を調べ、それを基に探っていけば、安定paretian族分布が理解されるに至っていない理由を見つけだすことができるだろう。しかし、はっきりとした答えが解明されておらず、これを議論するとなると複雑なうえ時間もかかるため、ここでそれを行うのは時間の無駄である。だからといって、探究そのものが無駄だと言っているわけではない。要するに、本書の範囲を越えた内容になるので、徹底究明は他書にゆずろうというわけである。
同様の理由で、市場の非線形性やカオス、マネーマネジメント用エキスパートシステムといった概念にも本書では触れない。これらが議論に値しないというわけではなく、題材そのものがそれぞれに本一冊分を割いて扱われるべき内容だからである。
また本書では変数を表すのにギリシャ文字は用いない。私がプログラミングを始めたのは70年代で、使った言語はFORTRANだった。ラッキーなことに、当時のキーボードにはギリシャ文字はなかった。今でもキーボードはギリシャ文字には対応しておらず、将来もそうであることを願っている。ギリシャ文字を使ったからといって、数式そのものが分かりやすくなるわけではなく、むしろ逆効果にしかならないからである。
◆本書の構成
第1章では、確率過程とギャンブル理論について説明する。これは、定量的アプローチという視点からトレーディングシステムを考えるための基礎となる。第2章では、トレーディングシステムについて見ていくと同時に、システムを将来のトレードに安心して使える信頼性の高いものにするにはどうすればよいかについて考える。第3章では、前の2つの章で学習したことを基に、収益の再投資の性質について考える。幾何的成長の概念もこの章から登場する。
第4章は本書の中で最も重要な章である。この章ではオプティマルfを中心に議論を進める。オプティマルfは、任意の確率分布に従う離散的な結果の流列から最大の幾何的成長を得るためのテクニックである(ただし、これらの離散的な結果は総合的に見ると有利であるものと仮定する)。例えば、ロサンジェルスのダウンタウンの気温を測定する温度計があったとしよう。気温は1日を通じて連続的に変化するが、測定するのは一定時間おき、例えば、1時間おきである。こういった1時間おきの測定値を、離散的な測定値と呼ぶ。これらはいわば、ひとつひとつが小さな「パケット」であり、連続関数のサンプリングによって得られるサンプルと考えてもらえばよいだろう。ルーレットゲームの結果が離散的であるのと同じように、トレーディングシステムが生み出すトレード流列もまた離散的である(ただし、トレード流列は連続関数から得られるわけではないことに注意)。
第5章は破産確率の計算方法について説明する。第6章では、最適な分散化を図るためのオプティマルfの組み合わせ方法について見ていく。これによって、どのシステムを選び、それぞれのシステムでどれくらいの量トレードすればよいかを数値的に算出することが可能になる。そして第7章は、本書に関連する内容でそれまでにカバーしきれなかった事柄を補足説明するとともに、それまでの内容を簡単にまとめる。また巻末の付録では、本書で扱う公式、興味深いタスクを実行するためのコンピュータープログラムをはじめ、そのまま実装できるプログラムもいくつか紹介する。
◆自明のことほど見落とされる
本書を読了した読者は、本書で提示された概念がすべて疑う余地のないものであることに気づくはずだ。それなのに、なぜ今までトレードの選択ばかりに気をとられ、本書で提示されているような「マネーマネジメント」概念に十分配慮してこなかったのか、と不思議に感じる読者もいることだろう。健全なトレーディングプログラムを作成するうえでこれらの概念がいかに重要であるかは、本書を通じて数学的に理解できるようになるだろう。
これらのテクニックがトレーダーたちにあまり重視されていないのには、理由がある。数学的に自明なことは見落とされることが多いのが現実なのである。例えば、イギリスなど左側通行の国を除く右側通行の国の交通規則について考えてみよう。車が左折しようと思った場合、左折車は対向車を優先させなければならない。
その左折車をはじめ、同じ車線にいるすべての後続車が、対向車線の車がすべて通過し終えるまで待たなければならないとすると、現行のこの左折規則の下では、「渋滞量」はおよそA*Bカーユニットである(ただし、Aは左折車と同じ車線にいる車の台数[左折車を含む]、Bは対向車線の車の台数とする。「渋滞量」とは、車一台が通過待ちしなければならない台数を各車について合計したものと定義し、その単位を「カーユニット」とする)。
さて今度は、左折車が優先通行権を与えられた場合を考えてみよう(2車線道路を想定。信号が赤から青に変わったら左折車が優先して通行できるものとする。また、左折車は方向指示器を点滅させているものとする)。この場合、渋滞量はおよそ1*Bカーユニットに減少する(ただし、Bは対向車線の車の台数を表す)。
例えば、対向車線に5台、左折車線に5台いるとすると、現行の左折規則の下での渋滞量は25カーユニットだが、代替案では渋滞量は5分の1に減少して5カーユニットになる。したがって、後者のシナリオのほうが交通はスムーズになることは明白だ。交通渋滞量は指数関数なので、交通量が多いほど交通がスムーズになる割合は高まる。
これほど素晴らしいアイデアがあるにもかかわらず、これまでに導入が検討されたことがあっただろうか。つまりここで言いたいのは、物事を行う手法には、いまだ提示されておらずとも、うまく機能し、もっともだと思えるより優れた手法が他にもあるということなのである。
◆初心者のための本ではない
本書は、儲かるトレーディングテクニックをすでに身につけているトレーダーを対象とするものである。そういった意味では、本書は初心者のための本ではないと言わなければならない。これは、本書読了後であれば理解していただけるはずだ。

 『投資家のためのマネーマネジメント
『投資家のためのマネーマネジメント



「ラルフ・ビンスの本は、内容の素晴らしさもさることながら、その存在自体に意義がある。ギャンブルと投資というまったく異なる2つの世界を融合させた書籍はこれまでに例がなく、彼は本書でそれを見事にやり遂げている。投資家たちはこれまでギャンブルの世界を自分たちとは無縁のものとして無視し続けてきた。当然ながら、そこから得られる貴重な教訓に目を向けることもなかった。投資家たちは気づいていないかもしれないが、ギャンブラーたちからは学ぶべき多くのことがある。今こそ彼らに注目するときではないだろうか。本書はそのための指南書である」



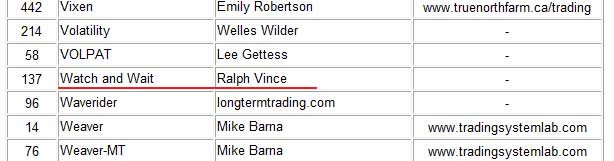 ◎ラルフ・ビンスの作成した売買システム「Watch and Wait」が、
◎ラルフ・ビンスの作成した売買システム「Watch and Wait」が、![]() が運営するトレーディングシステムのテストと評価を行う業界最有力ニュースレター『フューチャーズ・トゥルース(Futures Truth)』に登録されています。
が運営するトレーディングシステムのテストと評価を行う業界最有力ニュースレター『フューチャーズ・トゥルース(Futures Truth)』に登録されています。

